
| Bad Astronomy |
|
|
|
BA Blog
|
|
Q & BA
|
|
Bulletin Board
|
| Media |
|
|
|
Bitesize Astronomy
|
|
Bad Astro Store
|
|
Mad Science
|
|
Fun Stuff
|
| Site Info |
|
|
|
Links
|
| RELATED SITES |
| - Universe Today |
| - APOD |
| - The Nine Planets |
| - Mystery Investigators |
| - Slacker Astronomy |
| - Skepticality |
Buy My Stuff

Keep Bad Astronomy close to your heart, and help make me
filthy rich. Hey, it's either this or one of those really
irritating PayPal donation buttons here.
The Math of The Mummy Returns
So, how did I do that fancy math to figure out how fast the shadow moves? Well, remember in high school when your math teacher told you that someday math might save your life? Well, here is where Rick O'Connell should have paid attention in school (with apologies to the character Val Kilmer plays in Red Planet).
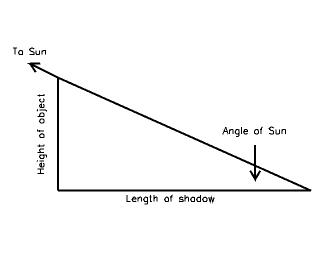 To the right you can see a diagram of how a shadow is cast by an object.
The length of the shadow depends on the height of an object (like a mountain
or a human) and how high up the Sun is. If the Sun is low, shadows are long.
If the Sun is high, shadows are short. If the Sun is on the horizon, shadows
are infinitely long, and if the Sun is straight up, shadows have a length
of zero.
To the right you can see a diagram of how a shadow is cast by an object.
The length of the shadow depends on the height of an object (like a mountain
or a human) and how high up the Sun is. If the Sun is low, shadows are long.
If the Sun is high, shadows are short. If the Sun is on the horizon, shadows
are infinitely long, and if the Sun is straight up, shadows have a length
of zero.
Here's where the trig comes in. We can calculate the length of the shadow if we know the Sun's angle above the horizon and the object's height. In this case, the length equals the height divided by the tangent of the Sun's angle:
We have to be careful, because the Sun has to clear the mountains first. O'Connell won't see the Sun until it rises over the mountains. At what angle does the Sun clear the mountains? We can use the above equation to solve for the angle:
Assuming the mountains are one kilometer high and 10 away, that means that
or, the Sun must be 5.7 degrees above the horizon to clear those mountains.
So where does that leave us? Well, we know how high up the Sun is, and the length of the mountains' shadow at that point (10 kilometers). So the next question is, how fast is the shadow moving?
There are two ways to do this. You could take a calculator, plug in different angles (say, increasing by one degree each time) and get the shadow length. The Earth spins 360 degrees in 24 hours, which means it spins 1 degree in 4 minutes; that in turn means the Sun moves 1 degree every 4 minutes in the sky. You can then convert your numbers into a velocity.
Or, you can do a bit more clever math. The shadow length depends on the Sun angle, so the change in the length depends on the change in that angle. That means you can take a derivative! If you figure out how the length changes with time, you get
where, yes, that's the co-secant of the angle. Luckily, I can program a computer to calculate this for me, and let the angle start at 5.7 degrees and run it up to where the Sun is way up the sky. If I do that, I get the following graph.
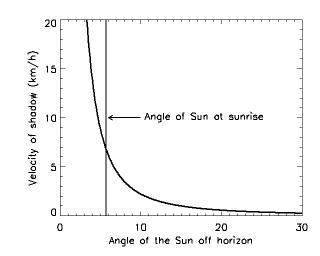 Note that when the Sun clears the mountains, the shadow lengths
are moving at a paltry
7 km/hr (5 mph). So really, Rick could have almost outwalked
the shadow line! He's
lucky those mountains were there; if they were farther away or lower,
the shadow
line would move faster. Also, as I noted on the main review page, the movie
actually had it wrong by having the line move too fast, not too slow.
Note that when the Sun clears the mountains, the shadow lengths
are moving at a paltry
7 km/hr (5 mph). So really, Rick could have almost outwalked
the shadow line! He's
lucky those mountains were there; if they were farther away or lower,
the shadow
line would move faster. Also, as I noted on the main review page, the movie
actually had it wrong by having the line move too fast, not too slow.
|
|
 |